
В. Жалнераускаса (UP2NV).
"Радио" 1-2 1982г.
![]() Коротковолновики и ультракоротковолновики, занимающиеся конструированием спортивной аппаратуры, знают, что применение высокочастотных кварцевых фильтров дает возможность существенно упростить трансивер, приемник или передатчик. Однако самостоятельно изготовить такой фильтр с приемлемыми для связной аппаратуры характеристиками в любительских условиях достаточно трудно. Дело в том, что для получивших наибольшее распространение и подробно описанных в литературе дифференциально-мостовых фильтров необходимы кварцевые резонаторы со строго определенным разносом резонансных частот. Подобные резонаторы заводского изготовления крайне редко оказываются в распоряжении радиолюбителя. Самостоятельная подгонка частоты имеющихся резонаторов, к которой обычно прибегают радиолюбители, требует определенного навыка и, как правило, ухудшает параметры резонаторов. Это в итоге сказывается на характеристиках фильтра в целом. Более того, дифференциально-мостовые фильтры, в принципе, требуют тщательного налаживания, что невозможно без соответствующей измерительной аппаратуры.
Коротковолновики и ультракоротковолновики, занимающиеся конструированием спортивной аппаратуры, знают, что применение высокочастотных кварцевых фильтров дает возможность существенно упростить трансивер, приемник или передатчик. Однако самостоятельно изготовить такой фильтр с приемлемыми для связной аппаратуры характеристиками в любительских условиях достаточно трудно. Дело в том, что для получивших наибольшее распространение и подробно описанных в литературе дифференциально-мостовых фильтров необходимы кварцевые резонаторы со строго определенным разносом резонансных частот. Подобные резонаторы заводского изготовления крайне редко оказываются в распоряжении радиолюбителя. Самостоятельная подгонка частоты имеющихся резонаторов, к которой обычно прибегают радиолюбители, требует определенного навыка и, как правило, ухудшает параметры резонаторов. Это в итоге сказывается на характеристиках фильтра в целом. Более того, дифференциально-мостовые фильтры, в принципе, требуют тщательного налаживания, что невозможно без соответствующей измерительной аппаратуры.
![]() В последнее время радиолюбители все чаще используют высокочастотные кварцевые фильтры, выполненные по так называемым лестничным схемам. Основное достоинство подобных фильтров — применение одинаковых кварцевых резонаторов, что существенно упрощает их изготовление. Как показывает практика, характеристики фильтра оказываются весьма близкими к расчетным, и он не требует дополнительного налаживания перед установкой в аппаратуру. Разумеется, сказанное здесь справедливо лишь в том случае, если расчет был выполнен правильно (в частности, были точно известны или измерены параметры резонаторов).
В последнее время радиолюбители все чаще используют высокочастотные кварцевые фильтры, выполненные по так называемым лестничным схемам. Основное достоинство подобных фильтров — применение одинаковых кварцевых резонаторов, что существенно упрощает их изготовление. Как показывает практика, характеристики фильтра оказываются весьма близкими к расчетным, и он не требует дополнительного налаживания перед установкой в аппаратуру. Разумеется, сказанное здесь справедливо лишь в том случае, если расчет был выполнен правильно (в частности, были точно известны или измерены параметры резонаторов).
![]() О том, что представляют собой лестничные кварцевые фильтры на одинаковых резонаторах, как их можно самостоятельно рассчитать и изготовить, рассказывается в статье известного советского коротковолновика Владаса Жалнераускаса (UP2NV).
О том, что представляют собой лестничные кварцевые фильтры на одинаковых резонаторах, как их можно самостоятельно рассчитать и изготовить, рассказывается в статье известного советского коротковолновика Владаса Жалнераускаса (UP2NV).
![]() При расчете кварцевых узкополосных фильтров обычно задаются средней частотой, полосой пропускания и коэффициентом прямоугольности амплитуд-но-частотной характеристики (АЧХ). Расчет начинают с определения необходимого числа кварцевых резонаторов, при котором будет обеспечен заданный коэффициент прямоугольности АЧХ. Этот анализ удобно проводить на основе фильтров-прототипов нижних частот (НЧ). Фильтры НЧ хорошо изучены, нормированные значения их элементов рассчитаны практически на все случаи и приведены в виде таблиц в справочниках по расчету фильтров (см.например, [1] — [3]).
При расчете кварцевых узкополосных фильтров обычно задаются средней частотой, полосой пропускания и коэффициентом прямоугольности амплитуд-но-частотной характеристики (АЧХ). Расчет начинают с определения необходимого числа кварцевых резонаторов, при котором будет обеспечен заданный коэффициент прямоугольности АЧХ. Этот анализ удобно проводить на основе фильтров-прототипов нижних частот (НЧ). Фильтры НЧ хорошо изучены, нормированные значения их элементов рассчитаны практически на все случаи и приведены в виде таблиц в справочниках по расчету фильтров (см.например, [1] — [3]).
![]() При расчете кварцевых фильтров обычно используют фильтры-прототипы либо с Чебышевской, либо с Батервортовской характеристикой затухания (см. соответственно рис. 1, а и рис. 1,б).
При расчете кварцевых фильтров обычно используют фильтры-прототипы либо с Чебышевской, либо с Батервортовской характеристикой затухания (см. соответственно рис. 1, а и рис. 1,б).
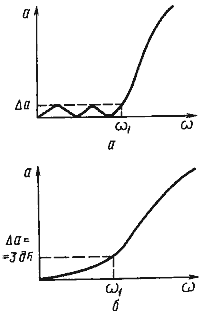
![]() Чебышевская характеристика имеет колебательный характер в полосе пропускания и монотонный в полосе задерживания, Батервортовская — монотонный характер как в полосе пропускания, так и полосе задерживания. Для приемо-передающей аппаратуры предпочтительнее фильтры с Чебышевской характеристикой, так как коэффициент прямоугольности АЧХ у них выше, чем у Батервортовских фильтров. Если же аппаратура предназначается для приема быстродействующих телеграфных сигналов, то желательно использовать фильтры с Батервортовской характеристикой, поскольку они "звенят" меньше фильтров с Чебышевской характеристикой.
Чебышевская характеристика имеет колебательный характер в полосе пропускания и монотонный в полосе задерживания, Батервортовская — монотонный характер как в полосе пропускания, так и полосе задерживания. Для приемо-передающей аппаратуры предпочтительнее фильтры с Чебышевской характеристикой, так как коэффициент прямоугольности АЧХ у них выше, чем у Батервортовских фильтров. Если же аппаратура предназначается для приема быстродействующих телеграфных сигналов, то желательно использовать фильтры с Батервортовской характеристикой, поскольку они "звенят" меньше фильтров с Чебышевской характеристикой.
![]() Допустимое значение неравномерности АЧХ в полосе пропускания выбирают, исходя из назначения фильтра и требований к его сложности. Увеличение допуска на неравномерность АЧХ в полосе пропускания приводит к увеличению затухания в полосе задерживания. Это позволяет с меньшим числом резонаторов обеспечить требуемый коэффициент прямоугольности АЧХ. В кварцевых фильтрах, которые будут использоваться в качестве основного фильтра SSB или CW сигналов в приемо-передающей аппаратуре, вполне допустима неравномерность до 1 дБ.
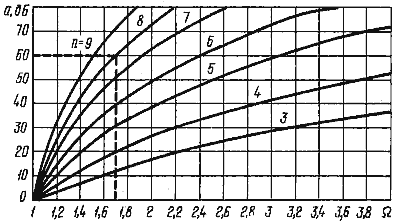
На рис. 2 приведены так называемые нормированные частотные характеристики затухания фильтров НЧ Чебышева 3 — 9-го порядка с неравномерностью АЧХ в полосе пропускания до 0.28 дБ.
Допустимое значение неравномерности АЧХ в полосе пропускания выбирают, исходя из назначения фильтра и требований к его сложности. Увеличение допуска на неравномерность АЧХ в полосе пропускания приводит к увеличению затухания в полосе задерживания. Это позволяет с меньшим числом резонаторов обеспечить требуемый коэффициент прямоугольности АЧХ. В кварцевых фильтрах, которые будут использоваться в качестве основного фильтра SSB или CW сигналов в приемо-передающей аппаратуре, вполне допустима неравномерность до 1 дБ.
На рис. 2 приведены так называемые нормированные частотные характеристики затухания фильтров НЧ Чебышева 3 — 9-го порядка с неравномерностью АЧХ в полосе пропускания до 0.28 дБ.
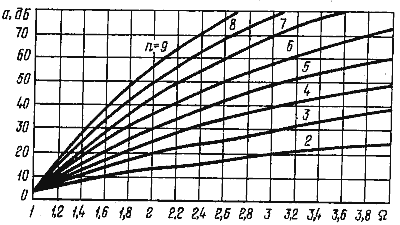
![]() Нормированные характеристики затухания фильтров НЧ Батерворта приведены на рис. 3.
Нормированные характеристики затухания фильтров НЧ Батерворта приведены на рис. 3.
![]() Нормирование произведено путем преобразования W=w/w1, где w1 — угловая частота среза АЧХ фильтра.
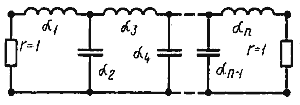
Нормированные значения элементов фильтра для схемы на рис. 4 приведены в табл. 1 и 2.
Нормирование произведено путем преобразования W=w/w1, где w1 — угловая частота среза АЧХ фильтра.
Нормированные значения элементов фильтра для схемы на рис. 4 приведены в табл. 1 и 2.
![]() Значение реактивных элементов фильтров НЧ Чебышева при неравномерности АЧХ 0.28 дБ
Значение реактивных элементов фильтров НЧ Чебышева при неравномерности АЧХ 0.28 дБ
Таблица №1
| n | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
| 3 | 1,345 | 1,141 | 1,345 | - | - | - | - | - | - |
| 4 | 1,146 | 1,513 | 1,513 | 1,146 | - | - | - | - | - |
| 5 | 1,456 | 1,307 | 2,283 | 1,307 | 1,456 | - | - | - | - |
| 6 | 1,277 | 1,528 | 1,878 | 1,878 | 1,528 | 1,277 | - | - | - |
| 7 | 1,488 | 1,343 | 2,388 | 1,451 | 2,388 | 1,343 | 1,488 | - | - |
| 8 | 1,340 | 1,508 | 2,019 | 1,844 | 1,844 | 2,019 | 1,508 | 1,340 | - |
| 9 | 1,502 | 1,357 | 2,420 | 1,481 | 2,480 | 1,481 | 2,420 | 1,357 | 1,502 |
![]() Значение реактивных элементов фильтров НЧ Батерворта
Значение реактивных элементов фильтров НЧ Батерворта
Таблица №2
| n | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 |
| 2 | 1,414 | 1,414 | - | - | - | - | - | - | - |
| 3 | 1,000 | 2,000 | 1,000 | - | - | - | - | - | - |
| 4 | 0,7654 | 1,848 | 1,848 | 0,7654 | - | - | - | - | - |
| 5 | 0,6180 | 1,618 | 2,000 | 1,618 | 0,6180 | - | - | - | - |
| 6 | 0,5176 | 1,414 | 1,932 | 1,932 | 1,414 | 0,5176 | - | - | - |
| 7 | 0,4450 | 1,247 | 1,802 | 2,000 | 1,802 | 1,247 | 0,4450 | - | - |
| 8 | 0,3902 | 1,111 | 1,663 | 1,962 | 1,962 | 1,663 | 1,111 | 0,3902 | - |
| 9 | 0,3473 | 1,000 | 1,532 | 1,879 | 2.000 | 1.879 | 1,532 | 1,000 | 0,3473 |
![]() Реальные значения рассчитывают по формулам Сi=ai /w1R и Lj=aj R/w1 (ai ,aj — нормированные значения реактивных элементов, R — реальное значение сопротивления нагрузки фильтра).
По приведенным на рис. 2 и 3 характеристикам можно выбрать подходящий тип фильтра-прототипа и его порядок При преобразовании фильтра-прототипа НЧ в кварцевый фильтр число кварцев в нем равно порядку (числу реактивных элементов) исходного фильтра.
Реальные значения рассчитывают по формулам Сi=ai /w1R и Lj=aj R/w1 (ai ,aj — нормированные значения реактивных элементов, R — реальное значение сопротивления нагрузки фильтра).
По приведенным на рис. 2 и 3 характеристикам можно выбрать подходящий тип фильтра-прототипа и его порядок При преобразовании фильтра-прототипа НЧ в кварцевый фильтр число кварцев в нем равно порядку (числу реактивных элементов) исходного фильтра.
![]() Если требуется прототип с числом элементов более девяти, то порядок фильтра увеличивают, повторяя в нем дополнительно необходимое число раз два средних элемента. Например, фильтр-прототип с десятью элементами можно получить на основе 9-элементного фильтра. Для этого исходный фильтр разъединяют между пятым и шестым элементами и в разрыв включают дополнительный элемент, аналогичный пятому. В фильтре-прототипе 11-го порядка в разрыв 9-элементного фильтра должны быть включены два дополнительных элемента, равных по значению соответственно четвертому и пятому. Описанная методика является приближенной, но достаточно точной для практических целей.
Если требуется прототип с числом элементов более девяти, то порядок фильтра увеличивают, повторяя в нем дополнительно необходимое число раз два средних элемента. Например, фильтр-прототип с десятью элементами можно получить на основе 9-элементного фильтра. Для этого исходный фильтр разъединяют между пятым и шестым элементами и в разрыв включают дополнительный элемент, аналогичный пятому. В фильтре-прототипе 11-го порядка в разрыв 9-элементного фильтра должны быть включены два дополнительных элемента, равных по значению соответственно четвертому и пятому. Описанная методика является приближенной, но достаточно точной для практических целей.
![]() При замене в фильтре НЧ всех конденсаторов параллельными колебательными контурами, а катушек индуктивности — последовательными он преобразуется в полосовой фильтр. Реальные значения элементов параллельных контуров определяют по формулам рис. 1
При замене в фильтре НЧ всех конденсаторов параллельными колебательными контурами, а катушек индуктивности — последовательными он преобразуется в полосовой фильтр. Реальные значения элементов параллельных контуров определяют по формулам рис. 1
![]() Сi=ai /R(w1-w-1)
Сi=ai /R(w1-w-1)
![]() Li=1/w02Ci
Li=1/w02Ci
![]() а последовательных —
а последовательных —
![]() Сj=1/w02Lj
Сj=1/w02Lj
![]() Lj=aj R/(w1-w-1)
Lj=aj R/(w1-w-1)
![]() где w1 и w-1 — граничные частоты полосы пропускания, а w0= (w1w-1)1/2.
где w1 и w-1 — граничные частоты полосы пропускания, а w0= (w1w-1)1/2.
![]() Схема полосового фильтра, преобразованная из фильтра НЧ, показана на рис. 5.
Схема полосового фильтра, преобразованная из фильтра НЧ, показана на рис. 5.
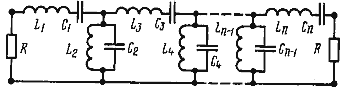
![]() Согласно определению, коэффициент прямоугольности АЧХ Кп равен отношению расстройки фильтра Dw , для узкополосных фильтров Dw = 2(w - w0), при котором обеспечивается заданное затухание, к полосе пропускания. В случае применения узкополосных фильтров Kп = W, и его определяют из графиков на рис. 2 и 3.
Согласно определению, коэффициент прямоугольности АЧХ Кп равен отношению расстройки фильтра Dw , для узкополосных фильтров Dw = 2(w - w0), при котором обеспечивается заданное затухание, к полосе пропускания. В случае применения узкополосных фильтров Kп = W, и его определяют из графиков на рис. 2 и 3.
![]() Полосовой фильтр, содержащий как параллельные, так и последовательные колебательные контуры, можно преобразовать в эквивалентный по АЧХ фильтр, содержащий только последовательные контуры. Для этого используется инвертор — преобразователь сопротивлений. Под инвертором понимается некий четырехполюсник, который, будучи нагруженным на линейную цепь, ведет себя как дуальная ей цепь с характеристической проводимостью, равной ее характеристическому сопротивлению.
Полосовой фильтр, содержащий как параллельные, так и последовательные колебательные контуры, можно преобразовать в эквивалентный по АЧХ фильтр, содержащий только последовательные контуры. Для этого используется инвертор — преобразователь сопротивлений. Под инвертором понимается некий четырехполюсник, который, будучи нагруженным на линейную цепь, ведет себя как дуальная ей цепь с характеристической проводимостью, равной ее характеристическому сопротивлению.
Дуальная цепь — это дуально преобразованная цепь. Дуальные преобразования за ключаются в замене последовательных соединенний параллельными, параллельных — последовательными, элементов цепи — дуальными элементами. Дуальными по отношению друг к другу являются индуктивность и емкость, сопротивление и проводимость.
![]() При наличии инвертора параллельные контуры в поперечных ветвях (за инвертором) ведут себя как последовательные в продольных ветвях (и наоборот). Значения элементов последовательных контуров в продольных ветвях (Lпр, Спр) взаимосвязаны с элементами параллельных контуров в поперечных цепях (Lпп, Cпп) через коэффициент инверсии K:
При наличии инвертора параллельные контуры в поперечных ветвях (за инвертором) ведут себя как последовательные в продольных ветвях (и наоборот). Значения элементов последовательных контуров в продольных ветвях (Lпр, Спр) взаимосвязаны с элементами параллельных контуров в поперечных цепях (Lпп, Cпп) через коэффициент инверсии K:
![]() Lпр = K2Cпп
Lпр = K2Cпп
![]() Cпр = Lпп/K2
Cпр = Lпп/K2
![]() Как видно из формул (1), инвертор обладает свойствами и идеального трансформатора с коэффициентом трансформации, равным коэффициенту инверсии. Вводя в полосовой фильтр (см. рис. 5) инверторы можно получить фильтр. состоящий только из последовательных контуров в продольных ветвях, причем характеристические сопротивления этих контуров можно сделать одинаковыми. Схема такого фильтра показана на рис. 6.
Как видно из формул (1), инвертор обладает свойствами и идеального трансформатора с коэффициентом трансформации, равным коэффициенту инверсии. Вводя в полосовой фильтр (см. рис. 5) инверторы можно получить фильтр. состоящий только из последовательных контуров в продольных ветвях, причем характеристические сопротивления этих контуров можно сделать одинаковыми. Схема такого фильтра показана на рис. 6.
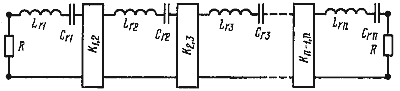
![]() Согласно определению инвертора схемы на рис. 5 и рис, 6 эквивалентны, если выполняются условия:
Согласно определению инвертора схемы на рис. 5 и рис, 6 эквивалентны, если выполняются условия:
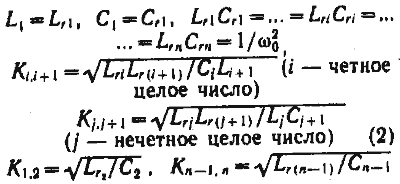
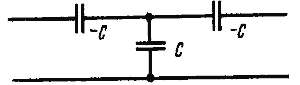
![]() Идеальных инверторов не существует. Однако при узких относительных полосах пропускания в качестве инвертора можно использовать узел, содержащий две отрицательные емкости (рис 7). Коэффициент инверсии К этого узла
Идеальных инверторов не существует. Однако при узких относительных полосах пропускания в качестве инвертора можно использовать узел, содержащий две отрицательные емкости (рис 7). Коэффициент инверсии К этого узла
![]() K = 1/wС
K = 1/wС ![]() (3)
(3)
![]() Практически этот узел можно реализовать потому, что при включении его в полосовой фильтр отрицательные емкости инвертора включаются в последовательные колебательные контуры. А несколько последовательно соединенных емкостей можно заменить одной, реактивное сопротивление которой равно алгебраической сумме реактивных сопротивлений заменяемых емкостей.
Практически этот узел можно реализовать потому, что при включении его в полосовой фильтр отрицательные емкости инвертора включаются в последовательные колебательные контуры. А несколько последовательно соединенных емкостей можно заменить одной, реактивное сопротивление которой равно алгебраической сумме реактивных сопротивлений заменяемых емкостей.
![]() Последовательные колебательные контуры в схеме на рис. 6 можно заменить кварцевыми резонаторами, поскольку характеры изменения их сопротивлений в области частот, близких к частоте первого резонанса кварца (для высокочастотных резонаторов — несколько килогерц от частоты резонанса), аналогичны. Но для такой замены необходимо несколько преобразовать схему фильтра, добиваясь, чтобы реальные значения реактивных элементов последовательных контуров и эквивалентной схемы кварцевого резонатора стали равными. Это возможно при условии, что
Последовательные колебательные контуры в схеме на рис. 6 можно заменить кварцевыми резонаторами, поскольку характеры изменения их сопротивлений в области частот, близких к частоте первого резонанса кварца (для высокочастотных резонаторов — несколько килогерц от частоты резонанса), аналогичны. Но для такой замены необходимо несколько преобразовать схему фильтра, добиваясь, чтобы реальные значения реактивных элементов последовательных контуров и эквивалентной схемы кварцевого резонатора стали равными. Это возможно при условии, что
![]() Lr1 = ... = Lri = ... = Lrn = Lкв
Lr1 = ... = Lri = ... = Lrn = Lкв![]() (4)
где Lкв — индуктивность эквивалентной схемы резонатора.
(4)
где Lкв — индуктивность эквивалентной схемы резонатора.
![]() Условия (2) и (4) совместимы, когда
Условия (2) и (4) совместимы, когда
![]() Сr1 = ... = Сri = ... = Сrn
Сr1 = ... = Сri = ... = Сrn![]() (5)
(5)
![]() Заменив инверторы в схеме рис. 6 узлом рис. 7, рассмотрим несколько отдельных случаев при разных порядках исходного фильтра-прототипа НЧ.
Заменив инверторы в схеме рис. 6 узлом рис. 7, рассмотрим несколько отдельных случаев при разных порядках исходного фильтра-прототипа НЧ.
![]() 1. n = 2. Исходный фильтр (рис. 8, а) можно заменить двухрезонаторным кварцевым (рис. 8, б).
1. n = 2. Исходный фильтр (рис. 8, а) можно заменить двухрезонаторным кварцевым (рис. 8, б).
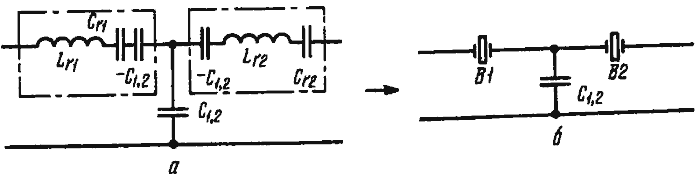
![]() Из рисунка следует, что
Из рисунка следует, что
![]() 1/Скв = 1/Сr - 1/С1,2
1/Скв = 1/Сr - 1/С1,2 ![]() (6)
(6)
![]() где Скв — емкость последовательного контура эквивалентной схемы кварцевого резонатора,
где Скв — емкость последовательного контура эквивалентной схемы кварцевого резонатора,
![]() 2. n = 3. Из исходной схемы (рис. 9, а) видно, что алгебраическая сумма емкостей среднего контура (-C1,2 , Cr, -С2,3) не равна сумме емкостей в крайних контурах.
2. n = 3. Из исходной схемы (рис. 9, а) видно, что алгебраическая сумма емкостей среднего контура (-C1,2 , Cr, -С2,3) не равна сумме емкостей в крайних контурах.
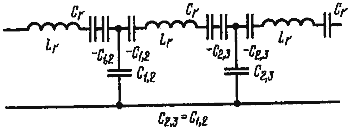
![]() Включив последовательно в крайние контуры дополнительные емкости -С2,3 , С2,3 и -C1,2 , C1,2 (рис. 9, б)
Включив последовательно в крайние контуры дополнительные емкости -С2,3 , С2,3 и -C1,2 , C1,2 (рис. 9, б)
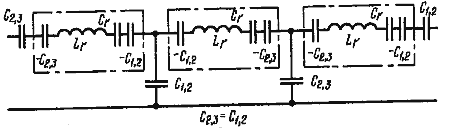
![]() получим схему трехрезонаторного фильтра (рис. 9, в).
получим схему трехрезонаторного фильтра (рис. 9, в).
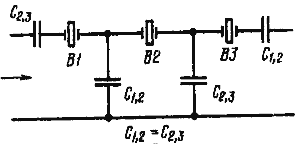
![]() При этом 1/Скв = 1/Сr - 1/С1,2
При этом 1/Скв = 1/Сr - 1/С1,2![]() (7)
(7)
![]() 3. n = 4. Исходная схема показана на рис. 10, а
3. n = 4. Исходная схема показана на рис. 10, а
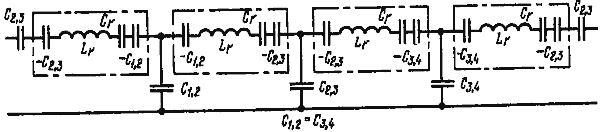
![]() преобразованная, четырехрезонаторного фильтра — на рис. 10, б.
преобразованная, четырехрезонаторного фильтра — на рис. 10, б.
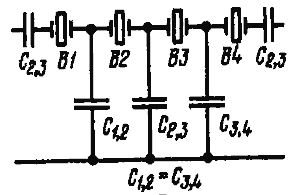
![]() Из рисунков следует, что
Из рисунков следует, что
![]() 1/Скв = 1/Сr - 1/С1,2 - 1/C2,3
1/Скв = 1/Сr - 1/С1,2 - 1/C2,3![]() (8)
(8)
![]() Методика измерения значений реактивных элементов эквивалентной схемы резонаторов была опубликована в "Радио" [4] и здесь не приводится. При известной Lкв можно рассчитывать емкости конденсаторов связи (инверторов) кварцевого фильтра. Из формулы (3) с учетом условий (2), (4), и (5), получаем
Методика измерения значений реактивных элементов эквивалентной схемы резонаторов была опубликована в "Радио" [4] и здесь не приводится. При известной Lкв можно рассчитывать емкости конденсаторов связи (инверторов) кварцевого фильтра. Из формулы (3) с учетом условий (2), (4), и (5), получаем
![]() Ввиду того, что согласно формулам (6) — (8), Сr<Скв средняя частота полосы пропускания фильтра получается выше частоты первого резонанса использованных кварцев. Однако учитывая узкополосность фильтров, при практических расчетах можно принимать w0 = wкв (wкв — угловая частота первого резонанса кварцевых резонаторов). Более точные результаты дает эмпирическая формула
Ввиду того, что согласно формулам (6) — (8), Сr<Скв средняя частота полосы пропускания фильтра получается выше частоты первого резонанса использованных кварцев. Однако учитывая узкополосность фильтров, при практических расчетах можно принимать w0 = wкв (wкв — угловая частота первого резонанса кварцевых резонаторов). Более точные результаты дает эмпирическая формула
![]() w0 = w + (w1 - w-1)/2
w0 = w + (w1 - w-1)/2 ![]() (10)
(10)
![]() Рассмотрим несколько случаев эволюции кварцевых фильтров из фильтров-прототипов НЧ с порядками выше четвертого.
Рассмотрим несколько случаев эволюции кварцевых фильтров из фильтров-прототипов НЧ с порядками выше четвертого.
![]() 1. n = 5. Из исходной схемы (рис. 11, а), в которую уже для выравнивания сопротивлений емкостей в контурах включены дополнительно емкости -С2,3 и С2,3 (по аналогии с предыдущими случаями), видно, что алгебраическая сумма сопротивлений емкостей среднего контура отличается от суммы сопротивлений емкостей других контуров.
1. n = 5. Из исходной схемы (рис. 11, а), в которую уже для выравнивания сопротивлений емкостей в контурах включены дополнительно емкости -С2,3 и С2,3 (по аналогии с предыдущими случаями), видно, что алгебраическая сумма сопротивлений емкостей среднего контура отличается от суммы сопротивлений емкостей других контуров.

![]() Поэтому в средний контур включают еще и отрицательную емкость С (рис. 11,б)
Поэтому в средний контур включают еще и отрицательную емкость С (рис. 11,б)
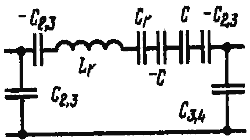
![]() и получают пятирезонаторный фильтр (рис. 11, в).
и получают пятирезонаторный фильтр (рис. 11, в).
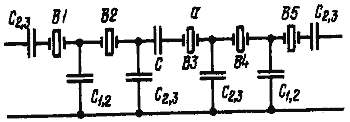
![]() Из схемы видно, что 1/С = 1/С1,2 - 1/С2,3.
Из схемы видно, что 1/С = 1/С1,2 - 1/С2,3.
![]() 2. n = 6. Схему шестирезонаторного фильтра (рис. 12) получают по аналогии с предыдущим случаем.
2. n = 6. Схему шестирезонаторного фильтра (рис. 12) получают по аналогии с предыдущим случаем.
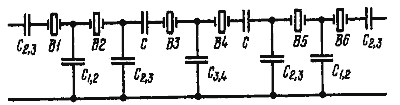
![]() При этом 1/С = 1/С1,2 - 1/С3,4.
При этом 1/С = 1/С1,2 - 1/С3,4.
![]() 3. n = 7. Для выравнивания сопротивлений емкостей во всех звеньях семирезонаторного фильтра (рис. 13) в среднее звено включают отрицательную емкость С1, в примыкающие — С2.
3. n = 7. Для выравнивания сопротивлений емкостей во всех звеньях семирезонаторного фильтра (рис. 13) в среднее звено включают отрицательную емкость С1, в примыкающие — С2.
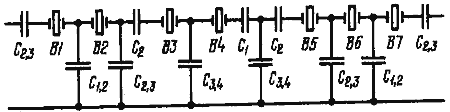
![]() В построенном фильтре
В построенном фильтре
![]() 1/С1 = 1/С1,2 + 1/С2,3 - 2/C3,4
1/С1 = 1/С1,2 + 1/С2,3 - 2/C3,4
![]() 1/С2 = 1/С1,2 - 1/С3,4.
1/С2 = 1/С1,2 - 1/С3,4.
![]() 4. n = 8. В отличие от предыдущего случая в восьми резонаторном фильтре (рис. 14) конденсатор С1 присутствует в двух смежных звеньях.
4. n = 8. В отличие от предыдущего случая в восьми резонаторном фильтре (рис. 14) конденсатор С1 присутствует в двух смежных звеньях.

![]() Емкости дополнительных конденсаторов С1 и С2 выбирают из условий, что
Емкости дополнительных конденсаторов С1 и С2 выбирают из условий, что
![]() 1/С1 = 1/С1,2 + 1/С2,3 - 1/C3,4 - 1/C4,5
1/С1 = 1/С1,2 + 1/С2,3 - 1/C3,4 - 1/C4,5
![]() 1/С1 = 1/С1,2 - 1/C3,4
1/С1 = 1/С1,2 - 1/C3,4 ![]() (11)
(11)
![]() Таким образом, можно построить схемы с любым числом кварцевых резонаторов.
Таким образом, можно построить схемы с любым числом кварцевых резонаторов.
![]() Как правило, в реальной приемопередающей аппаратуре кварцевый фильтр нагружен на узлы, обладающие некоторой емкостью, например, входной или выходной емкостью транзистора, емкостью экранированного провода. Емкостная нагрузка может заметно исказить АЧХ фильтра. Последовательные емкости на входе и выходе фильтра легко можно трансформировать в параллельные (рис. 16).
Как правило, в реальной приемопередающей аппаратуре кварцевый фильтр нагружен на узлы, обладающие некоторой емкостью, например, входной или выходной емкостью транзистора, емкостью экранированного провода. Емкостная нагрузка может заметно исказить АЧХ фильтра. Последовательные емкости на входе и выходе фильтра легко можно трансформировать в параллельные (рис. 16).
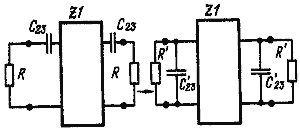
![]() Параллельная емкость С`2,3 на входе фильтра равна
Параллельная емкость С`2,3 на входе фильтра равна
![]() С`2,3 = С2,3/(1+ a2,32)
С`2,3 = С2,3/(1+ a2,32)
![]() При трансформации последовательной емкости в параллельную возрастает сопротивление нагрузки фильтра:
При трансформации последовательной емкости в параллельную возрастает сопротивление нагрузки фильтра:
![]() R`= R(1+ a2,32) где a2,3 — нормированное значение емкости С2,3
R`= R(1+ a2,32) где a2,3 — нормированное значение емкости С2,3
![]() a2,3 = w0RC2,3
a2,3 = w0RC2,3
![]() При установке фильтра в реальную конструкцию емкости нагрузки могут быть нейтрализованы соответствующим уменьшением емкости параллельно включенных на входе и выходе конденсаторов фильтра.
При установке фильтра в реальную конструкцию емкости нагрузки могут быть нейтрализованы соответствующим уменьшением емкости параллельно включенных на входе и выходе конденсаторов фильтра.
![]() Часто в приемо-передающей аппаратуре желательно иметь несколько различных полос пропускания. Строить отдельные фильтры для каждой требуемой полосы не всегда оправдано, так как возрастает число необходимых кварцевых резонаторов. Если порядок фильтра не превышает четырех, можно построить фильтр с переключаемой полосой пропускания (рис. 17).
Часто в приемо-передающей аппаратуре желательно иметь несколько различных полос пропускания. Строить отдельные фильтры для каждой требуемой полосы не всегда оправдано, так как возрастает число необходимых кварцевых резонаторов. Если порядок фильтра не превышает четырех, можно построить фильтр с переключаемой полосой пропускания (рис. 17).
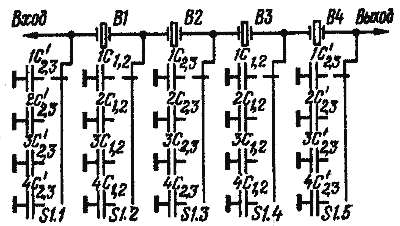
![]() При недостаточной избирательности четырехкристального фильтра можно последовательно включать несколько фильтров. В этим случае, чтобы не увеличилась неравномерность АЧХ в полосе пропускания, между фильтрами включают развязывающие цепи для согласования сопротивлений нагрузки или отдельные фильтры включают в разные каскады аппаратуры. Следует отметить, что изменение полосы пропускания влечет за собой и необходимость изменения сопротивления нагрузки фильтра. Поэтому при конструировании фильтра следует предусмотреть одновременное переключение полосы пропускания и нагрузки.
При недостаточной избирательности четырехкристального фильтра можно последовательно включать несколько фильтров. В этим случае, чтобы не увеличилась неравномерность АЧХ в полосе пропускания, между фильтрами включают развязывающие цепи для согласования сопротивлений нагрузки или отдельные фильтры включают в разные каскады аппаратуры. Следует отметить, что изменение полосы пропускания влечет за собой и необходимость изменения сопротивления нагрузки фильтра. Поэтому при конструировании фильтра следует предусмотреть одновременное переключение полосы пропускания и нагрузки.
![]() Согласно формулам (6) — (8) при переключении полосы пропускания одновременно изменяется средняя частота полосы пропускания, которую можно приблизительно рассчитать по эмпирической формуле (10). При изменении средней частоты нижняя граничная частота полосы пропускания остается близкой к частоте первого резонанса использованных кварцевых резонаторов, что позволяет такой же резонатор применить в опорном гетеродине приемо-передающей аппаратуры.
Согласно формулам (6) — (8) при переключении полосы пропускания одновременно изменяется средняя частота полосы пропускания, которую можно приблизительно рассчитать по эмпирической формуле (10). При изменении средней частоты нижняя граничная частота полосы пропускания остается близкой к частоте первого резонанса использованных кварцевых резонаторов, что позволяет такой же резонатор применить в опорном гетеродине приемо-передающей аппаратуры.
![]() Если желаемый коэффициент прямоугольности АЧХ не может быть достигнут с имеющимся числом кварцевых резонаторов, следует выбирать в качестве фильтра-прототипа фильтр Чебышева с большей неравномерностью в полосе пропускания. На рис. 18 показана взаимосвязь коэффициента прямоугольности АЧХ (— 60 дБ) с неравномерностью АЧХ в полосе пропускания для фильтра Чебышева 6-го порядка.
Если желаемый коэффициент прямоугольности АЧХ не может быть достигнут с имеющимся числом кварцевых резонаторов, следует выбирать в качестве фильтра-прототипа фильтр Чебышева с большей неравномерностью в полосе пропускания. На рис. 18 показана взаимосвязь коэффициента прямоугольности АЧХ (— 60 дБ) с неравномерностью АЧХ в полосе пропускания для фильтра Чебышева 6-го порядка.
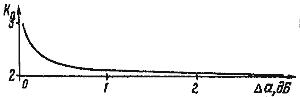
![]() Из рисунка видно, что повышение допуска на неравномерность АЧХ до 1 дБ заметно улучшает избирательные свойства фильтра. Дальнейшее повышение неравномерности АЧХ существенного выигрыша не дает. Фильтры-прототипы НЧ с неравномерностью АЧХ до 3 дБ даны, например, в [5].
Из рисунка видно, что повышение допуска на неравномерность АЧХ до 1 дБ заметно улучшает избирательные свойства фильтра. Дальнейшее повышение неравномерности АЧХ существенного выигрыша не дает. Фильтры-прототипы НЧ с неравномерностью АЧХ до 3 дБ даны, например, в [5].
![]() Все приведенные выше формулы пригодны и для расчета фильтров на механических гармониках. Однако необходимо отметить следующее. Из рис. 15 видно, что крутизна высокочастотного ската характеристики затухания кварцевого фильтра больше низкочастотного. Это объясняется рядом допущений, принятых при эволюции схемы кварцевого фильтра из фильтра-прототипа НЧ. При замещении последовательных контуров в схеме рис. 6 кварцевыми резонаторами пренебрегали наличием параллельной емкости Со в эквивалентной схеме кварцевого резонатора. Строго говоря, при наличии Со АЧХ кварцевого фильтра отклоняется от Чебышевской или Батервортской характеристики затухания. В области частот выше полосы пропускания появляется полюс бесконечного затухания, а в области частот ниже полосы пропускания затухание фильтра несколько снижается. Отклонение реальной характеристики затухания фильтра от Чебышевской или Батервортской тем больше, чем ближе полюс бесконечного затухания к полосе пропускания фильтра. В свою очередь это зависит от резонансного промежутка df кварцевых резонаторов (от разности частот последовательного f2 и параллельного f1 резонансов):
Все приведенные выше формулы пригодны и для расчета фильтров на механических гармониках. Однако необходимо отметить следующее. Из рис. 15 видно, что крутизна высокочастотного ската характеристики затухания кварцевого фильтра больше низкочастотного. Это объясняется рядом допущений, принятых при эволюции схемы кварцевого фильтра из фильтра-прототипа НЧ. При замещении последовательных контуров в схеме рис. 6 кварцевыми резонаторами пренебрегали наличием параллельной емкости Со в эквивалентной схеме кварцевого резонатора. Строго говоря, при наличии Со АЧХ кварцевого фильтра отклоняется от Чебышевской или Батервортской характеристики затухания. В области частот выше полосы пропускания появляется полюс бесконечного затухания, а в области частот ниже полосы пропускания затухание фильтра несколько снижается. Отклонение реальной характеристики затухания фильтра от Чебышевской или Батервортской тем больше, чем ближе полюс бесконечного затухания к полосе пропускания фильтра. В свою очередь это зависит от резонансного промежутка df кварцевых резонаторов (от разности частот последовательного f2 и параллельного f1 резонансов):
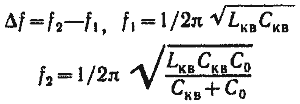
![]() Индуктивность эквивалентной схемы кварцевого резонатора не зависит от номера механической гармоники и остается постоянной, а емкость последовательного резонанса уменьшается. Следовательно, резонансный промежуток кварцевых резонаторов с ростом номера механической гармоники снижается. При большом значении Со, например у резонаторов старых типов, вообще не удается получить требуемую ширину полосы не только на гармониках, но и на основной частоте. Это объясняется
тем, что полюс бесконечного затухания получается в пределах требуемой полосы пропускания. Многие современные кварцевые резонаторы с высокой частотой резонанса на первой гармонике имеют достаточный резонансный промежуток, позволяющий использовать их в качестве элементов фильтра до пятой механической гармоники. Автором были построены кварцевые фильтры на частоте пятой механической гармоники 85 МГц с полосой пропускания 2.2 кГц. Измеренный резонансный промежуток составлял 3,4 кГц. Резонансный промежуток можно расширить подключением параллельно или последовательно к кварцевым резонаторам катушек индуктивности.
Индуктивность эквивалентной схемы кварцевого резонатора не зависит от номера механической гармоники и остается постоянной, а емкость последовательного резонанса уменьшается. Следовательно, резонансный промежуток кварцевых резонаторов с ростом номера механической гармоники снижается. При большом значении Со, например у резонаторов старых типов, вообще не удается получить требуемую ширину полосы не только на гармониках, но и на основной частоте. Это объясняется
тем, что полюс бесконечного затухания получается в пределах требуемой полосы пропускания. Многие современные кварцевые резонаторы с высокой частотой резонанса на первой гармонике имеют достаточный резонансный промежуток, позволяющий использовать их в качестве элементов фильтра до пятой механической гармоники. Автором были построены кварцевые фильтры на частоте пятой механической гармоники 85 МГц с полосой пропускания 2.2 кГц. Измеренный резонансный промежуток составлял 3,4 кГц. Резонансный промежуток можно расширить подключением параллельно или последовательно к кварцевым резонаторам катушек индуктивности.
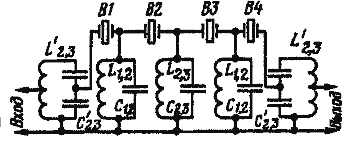
![]() Сложности возникают также и из-за того, что номиналы конденсаторов связи получаются весьма малыми, соизмеримыми с емкостью монтажа. Поэтому при конструировании кварцевых фильтров на частотах механических гармоник следует особенно продумать монтаж, по возможности применять малогабаритные детали. В фильтрах с шестью я более резонаторами цепи, содержащие выравнивающие емкости C1 и С2 (рис. 13, 14). лучше пересчитать из "звезды" в "треугольник" [6], что позволит несколько снизить емкость монтажа.
Сложности возникают также и из-за того, что номиналы конденсаторов связи получаются весьма малыми, соизмеримыми с емкостью монтажа. Поэтому при конструировании кварцевых фильтров на частотах механических гармоник следует особенно продумать монтаж, по возможности применять малогабаритные детали. В фильтрах с шестью я более резонаторами цепи, содержащие выравнивающие емкости C1 и С2 (рис. 13, 14). лучше пересчитать из "звезды" в "треугольник" [6], что позволит несколько снизить емкость монтажа.
![]() Радикальной мерой снижения влияния емкостей монтажа является использование параллельных колебательных контуров вместо конденсаторов связи. Соответственной расстройкой этих контуров можно получить желаемые реактивные емкостные сопротивления связи (инверторов). Вообще, если кварцевые фильтры, рассчитанные на частоту основной гармоники, не требуют никакой настройки и дают хорошее совпадение расчетных результатов с реальными характеристиками, то разработка фильтров на механических гармониках требует определенной экспериментальной работы.
На рис. 19 показана схема четырехкварцевого фильтра на частоту 85 МГц. Коэффициент прямоугольности (на уровне — 40 дБ) равен 2.8, потери в полосе пропускания —3 дБ, неравномерность АЧХ — 1 дБ.
Радикальной мерой снижения влияния емкостей монтажа является использование параллельных колебательных контуров вместо конденсаторов связи. Соответственной расстройкой этих контуров можно получить желаемые реактивные емкостные сопротивления связи (инверторов). Вообще, если кварцевые фильтры, рассчитанные на частоту основной гармоники, не требуют никакой настройки и дают хорошее совпадение расчетных результатов с реальными характеристиками, то разработка фильтров на механических гармониках требует определенной экспериментальной работы.
На рис. 19 показана схема четырехкварцевого фильтра на частоту 85 МГц. Коэффициент прямоугольности (на уровне — 40 дБ) равен 2.8, потери в полосе пропускания —3 дБ, неравномерность АЧХ — 1 дБ.
1. М. Е. Альбац. Справочник по расчету фильтров и линий задержки,— М.— Л., Госэнергоиздат, 1963.
2. Г. Ханзел. Справочник по расчету фильтров.— М., Советское радио. 1974.
3. Э. Христиан, Е. Энзенман. Таблицы и графики по расчету фильтров.— М., Связь. 1975.
4. Л. Лабутин. Кварцевые резонаторы.— Радио. 1975. № 3.
5. Г. Л. Маттей, Л. Янг. Е. М. Т. Джонск. Фильтры СВЧ. согласующие цепи и цепи связи.— М Связь, 1971.
6. П. М. Тодаров. Преобразование Т, П и Г-образных четырехполюсников.— Электросвязь, 1976. № 1.
![]()